Revise
Conditional Probability and Tree Diagrams
Conditional Probability and Tree Diagrams
Tree diagrams are visual ways of understanding probabilities involving more than one event. Conditional probability is the mathematical formulation of this understanding. Ultimately – both help us answer the same question: what is the probability of an event happening given that a related event has already happened?
Make sure you are happy with the following topics before continuing.
A Level Maths Predicted Papers 2025
The MME A level maths predicted papers are an excellent way to practise, using authentic exam style questions that are unique to our papers. Our examiners have studied A level maths past papers to develop predicted A level maths exam questions in an authentic exam format. The profit from every pack is reinvested into making free content on MME, which benefits millions of learners across the country.
View Product
A-A* A Level Maths Practice Papers
The MME A-A* A level maths practice papers are excellent for those top achieving students to practise for their exams, using authentic exam style questions that are unique to our practice papers. Our content experts have studied A level maths past papers and specifications to develop specific A-A* A level maths exam questions in an authentic exam style. The profit from every pack is reinvested into making free content on MME, which benefits millions of learners across the country.
View ProductTree Diagrams
Suppose we have two events, \color{red}A and \color{blue}B, such that \mathbb{P}(\color{red}A\color{grey})=\color{red}{p} and \mathbb{P}(\color{blue}B\color{grey})=\color{blue}{q}. A tree diagram for \color{red}A and \color{blue}B looks like this:
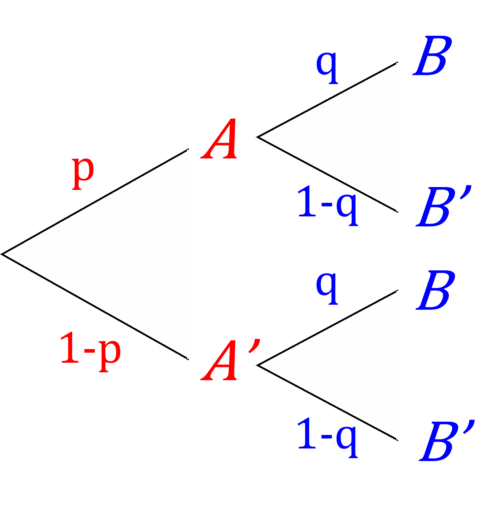
From this, we can see that:
\mathbb{P}(\color{red}A\color{grey}\cap\color{blue}B\color{grey})=\color{red}p\color{blue}q
\mathbb{P}(\color{red}A'\color{grey}\cap\color{blue}B\color{grey})=\color{red}(1-p)\color{blue}q
\mathbb{P}(\color{red}A\color{grey}\cap\color{blue}B'\color{grey})=\color{red}p\color{blue}(1-q)
\mathbb{P}(\color{red}A'\color{grey}\cap\color{blue}B'\color{grey})=\color{red}(1-p)\color{blue}(1-q)
(Note: For guidance on the notation used here please see Probability and Venn Diagrams.)
Conditional Probability
Conditional probability is the probability of an event happening given that a related event has already happened.
Notation: \color{grey}\mathbb{P}(\color{blue}B\color{grey}|\color{red}A\color{grey}) means the probability of \color{blue}B given \color{red}A which is the probability of \color{blue}B provided that \color{red}A has already happened.
We have the following formula:
\color{grey}\mathbb{P}(\color{blue}B\color{grey}|\color{red}A\color{grey})=\dfrac{\mathbb{P}(\color{red}A\color{grey}\cap\color{blue}B\color{grey})}{\mathbb{P}(\color{red}A\color{grey})}
If \color{blue}B is conditional on \color{red}A, then \color{red}A is conditional on \color{blue}B, and \color{grey}\mathbb{P}(\color{blue}B\color{grey}|\color{red}A\color{grey}) is linked to \color{grey}\mathbb{P}(\color{red}A\color{grey}|\color{blue}B\color{grey}) by the formula:
\color{grey}\mathbb{P}(\color{red}A\color{grey}|\color{blue}B\color{grey})=\dfrac{\mathbb{P}(\color{blue}B\color{grey}|\color{red}A\color{grey})\mathbb{P}(\color{red}A\color{grey})}{\mathbb{P}(\color{blue}B\color{grey}|\color{red}A\color{grey})\mathbb{P}(\color{red}A\color{grey})+\mathbb{P}(\color{blue}B\color{grey}|\color{red}A'\color{grey})\mathbb{P}(\color{red}A'\color{grey})}
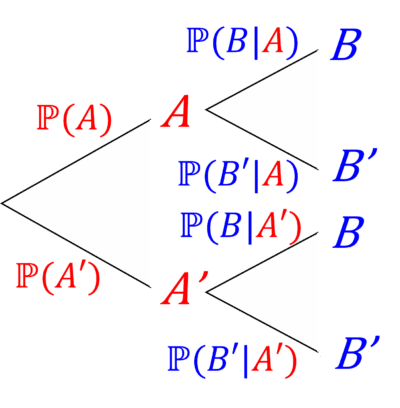
Using what we know about conditional probability, we can now redo the tree diagram:
Example 1: Tree Diagrams
Sally has a bag of sweets. There are 12 blue sweets and 18 red sweets in total. Sally takes two sweets, without replacement. What is the probability that she takes exactly one blue sweet.
[3 marks]
Draw a tree diagram:
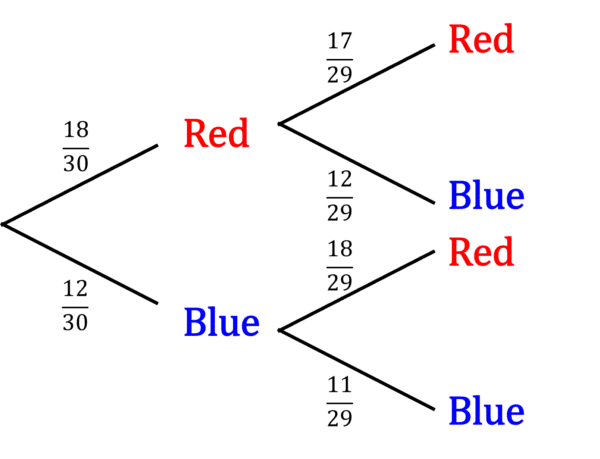
\mathbb{P}(\text{\color{red}Red\color{grey} and \color{red}Red\color{grey}})=\dfrac{18}{30}\times\dfrac{17}{29}=\dfrac{51}{145}
\mathbb{P}(\text{\color{red}Red\color{grey} and \color{blue}Blue\color{grey}})=\dfrac{18}{30}\times\dfrac{12}{29}=\dfrac{36}{145}
\mathbb{P}(\text{\color{blue}Blue\color{grey} and \color{red}Red\color{grey}})=\dfrac{12}{30}\times\dfrac{18}{29}=\dfrac{36}{145}
\mathbb{P}(\text{\color{blue}Blue\color{grey} and \color{blue}Blue\color{grey}})=\dfrac{12}{30}\times\dfrac{11}{29}=\dfrac{22}{145}
So the probability of one blue sweet is:
\mathbb{P}(\text{One blue sweet})=\dfrac{36}{145}+\dfrac{36}{145}=\dfrac{72}{145}
Example 2: Conditional Probability
Every morning Jonathan either has breakfast (B) or doesn’t (B'), then leaves the house (L) or doesn’t (L'). The probability that he has breakfast is 0.3. If he eats breakfast the probability that he leaves the house is 0.6. If he does not eat breakfast the probability that he leaves the house is 0.2. If you see Jonathan outside of his house, what is the probability he had breakfast?
[4 marks]
We want to find \mathbb{P}(B|L). We can use the formula:
\begin{aligned}\mathbb{P}(B|L)&=\dfrac{\mathbb{P}(L|B)\mathbb{P}(B)}{\mathbb{P}(L|B)\mathbb{P}(B)+\mathbb{P}(L|B')\mathbb{P}(B')}\\[1.2em]&=\dfrac{0.6\times 0.3}{0.6\times 0.3+0.2\times 0.7}\\[1.2em]&=\dfrac{0.18}{0.18+0.14}\\[1.2em]&=\dfrac{0.18}{0.32}\\[1.2em]&=\dfrac{9}{16}\\[1.2em]&=0.5625\end{aligned}
Note: We could also have done this question with a tree diagram.
Conditional Probability and Tree Diagrams Example Questions
Question 1: What is the probability of getting two heads when flipping a coin three times?
[4 marks]
For this, we need a tree diagram with three events.
\begin{aligned}&\mathbb{P}(\text{two heads})=\mathbb{P}(HHT)+\mathbb{P}(HTH)+\mathbb{P}(THH)\\[1.2em]&=0.5\times 0.5\times 0.5+0.5\times 0.5\times 0.5+0.5\times 0.5\times 0.5\\[1.2em]&=0.125+0.125+0.125\\[1.2em]&=0.375\end{aligned}
Question 2: \mathbb{P}(A|B)=0.6, \mathbb{P}(A\cap B)=0.3 and \mathbb{P}(B|A)=0.9
What are \mathbb{P}(A) and \mathbb{P}(B)?
[4 marks]
\mathbb{P}(B|A)=\dfrac{\mathbb{P}(A\cap B)}{\mathbb{P}(A)}
\begin{aligned}\mathbb{P}(A)&=\dfrac{\mathbb{P}(A\cap B)}{\mathbb{P}(B|A)}\\[1.2em]&=\dfrac{0.3}{0.9}\\[1.2em]&=\dfrac{1}{3}\end{aligned}
\mathbb{P}(A|B)=\dfrac{\mathbb{P}(A\cap B)}{\mathbb{P}(B)}
\begin{aligned}\mathbb{P}(B)&=\dfrac{\mathbb{P}(A\cap B)}{\mathbb{P}(A|B)}\\[1.2em]&=\dfrac{0.3}{0.6}\\[1.2em]&=\dfrac{1}{2}\end{aligned}
Question 3: Aditya owns a bag of 100 marbles. 39 of them are green and 61 of them are red. If he removes two without replacement, what is the probability of them both being the same colour?
[4 marks]
Use a tree diagram for this question.
\begin{aligned}\mathbb{P}(\text{same colour})&=\mathbb{P}(\text{red \& red})+\mathbb{P}(\text{green \& green})\\[1.2em]&=\dfrac{61}{100}\times\dfrac{60}{99}+\dfrac{39}{100}\times\dfrac{38}{99}\\[1.2em]&=\dfrac{61}{165}+\dfrac{247}{1650}\\[1.2em]&=\dfrac{857}{1650}\\[1.2em]&=0.519\end{aligned}
Question 4: Ellie takes the train to work. On a given day, the chances of the train being delayed are 0.5. If the train is on time, Ellie has a probability of 0.9 of arriving to work on time. If the train is delayed, Ellie has a probability of 0.8 of being late.
Ellie arrives at work on time on Tuesday. What is the probability that Tuesday’s train was on time?
[6 marks]
For this we use the big formula:
\mathbb{P}(A|B)=\dfrac{\mathbb{P}(B|A)\mathbb{P}(A)}{\mathbb{P}(B|A)\mathbb{P}(A)+\mathbb{P}(B|A')\mathbb{P}(A')}
Call A the event that Ellie’s train on time and call B the event that Ellie is on time. We want \mathbb{P}(A|B).
The question gives:
\mathbb{P}(A)=0.5
\mathbb{P}(A')=0.5
\mathbb{P}(B|A)=0.9
\mathbb{P}(B'|A)=0.1
\mathbb{P}(B'|A')=0.8
\mathbb{P}(B|A')=0.2
Now we put these values into the formula.
\begin{aligned}\mathbb{P}(A|B)&=\dfrac{0.9\times 0.5}{0.9\times 0.5+0.2\times 0.5}\\[1.2em]&=\dfrac{0.45}{0.45+0.1}\\[1.2em]&=\dfrac{0.45}{0.55}\\[1.2em]&=0.819\end{aligned}The probability that Tuesday’s train was on time is 0.819
Specification Points Covered
M2 – Understand and use conditional probability, including the use of tree diagrams, Venn diagrams, two-way tables, understand and use the conditional probability formula:
\mathbb{P}(A|B)=\dfrac{\mathbb{P}(A\cap B)}{\mathbb{P}B}
Related Topics
