Revise
Exponentials and Logarithms
Exponentials and Logarithms
A sum such as 4+3=7 has two inverses: 7-3=4 and 7-4=3.
A product such as 8\times6=48 has two inverses: 48\div6=8 and 48\div8=6.
An exponential (power) such as 3^{4}=81 has an inverse of the fourth root: \sqrt[4]{81}=3. But for the pattern to continue there must be another inverse – an operation involving 81 and 3 to get back to 4.
This other inverse is the logarithm.
A Level Maths Predicted Papers 2025
The MME A level maths predicted papers are an excellent way to practise, using authentic exam style questions that are unique to our papers. Our examiners have studied A level maths past papers to develop predicted A level maths exam questions in an authentic exam format. The profit from every pack is reinvested into making free content on MME, which benefits millions of learners across the country.
View Product
A-A* A Level Maths Practice Papers
The MME A-A* A level maths practice papers are excellent for those top achieving students to practise for their exams, using authentic exam style questions that are unique to our practice papers. Our content experts have studied A level maths past papers and specifications to develop specific A-A* A level maths exam questions in an authentic exam style. The profit from every pack is reinvested into making free content on MME, which benefits millions of learners across the country.
View Product
Logarithms are the Inverse of Exponentials
\log_{a}(b)=c means that a^{c}=b
a^{1}=a for any a so \log_{a}(a)=1
a^{0}=1 for any a so \log_{a}(1)=0
Example: \log_{3}(81)=4 because 3^{4}=81
We also have other rules:
\log_{a}(x)+\log_{a}(y)=\log_{a}(xy)
\log_{a}(x)-\log_{a}(y)=\log_{a}\left(\dfrac{x}{y}\right)
\log_{a}(x^{n})=n\log_{a}(x)
\log_{a}(x)=\dfrac{\log_{b}(x)}{\log_{b}(a)}
Note: The little number after the \text{log} is called the base. The most common base is 10, but this is usually left out – i.e. for \text{log}_{10} we just write \text{log} .
Using Logarithms and Exponentials to Solve Equations
We can use the rules above – called the laws of logarithms – to solve equations that involve exponentials.
Example: 3^{4x}=5
\log(3^{4x})=\log(5)
4x\log(3)=\log(5)
\begin{aligned}x&=\dfrac{\log(5)}{4\log(3)}\\[1.2em]&=0.366\end{aligned}
Note: The base of the logarithm was not given in this example. This is because we would get the same answer using any base.
On the flipside, we can use exponentials to solve equations involving logarithms.
Example: 6\log_{4}(x)=17
\log_{4}(x)=\dfrac{17}{6}
\begin{aligned}x&=4^{\frac{17}{6}}\\[1.2em]&=50.8\end{aligned}
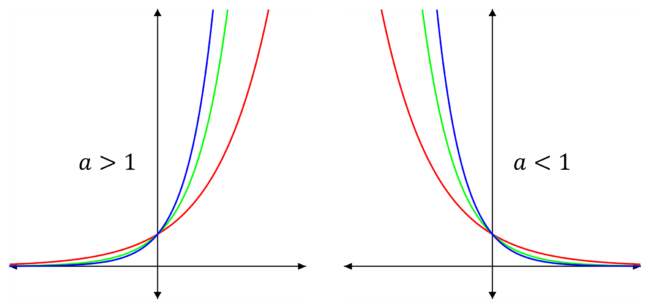
Graphs of Exponentials
An exponential graph is a graph of the function y=a^{x} for some a>0. They all have the same basic shape. If a>1 then y increases as x increases. If a<1 then y decreases as x increases. Larger a gives faster increase if a>1 while smaller a gives faster decrease if a<1.
Note: Exponential graphs never reach \mathbf{0}.
On the left graph is y=2^{x}, y=3^{x} and y=4^{x}.
On the right graph is y=\left(\dfrac{1}{2}\right)^{x}, y=\left(\dfrac{1}{3}\right)^{x} and y=\left(\dfrac{1}{4}\right)^{x}.
Exponentials and Logarithms Example Questions
Question 1: Write the following in logarithm notation:
a) 7^{3}=343
b) 5^{4}=625
c) 2^{16}=65536
d) 729^{\frac{1}{3}}=9
e) 22^{0}=1
[5 marks]
a) \log_{7}(343)=3
b) \log_{5}(625)=4
c) \log_{2}(65536)=16
d) \log_{729}(9)=\dfrac{1}{3}
e) \log_{22}(1)=0
Question 2: Evaluate:
a) \log_{2}(16)
b) \log_{5}(125)
c) \log_{3}(243)
d) \log_{\frac{1}{4}}\left(\dfrac{1}{16}\right)
[4 marks]
a) 4 because 2^{4}=16
b) 3 because 5^{3}=125
c) 5 because 3^{5}=243
d) 2 because \left(\dfrac{1}{4}\right)^{2}=\dfrac{1}{16}
Question 3: Write these expressions as a single logarithm:
a) \log_{a}(12)+\log_{a}(6)
b) 2\log_{b}(5)+\log_{b}(4)
c) 3\log_{6}(2)+\dfrac{1}{2}\log_{6}(9)
[3 marks]
a)
\begin{aligned}\log_{a}(12)+\log_{a}(6)&=\log_{a}(12\times6)\\[1.2em]&=\log_{a}(72)\end{aligned}
b)
\begin{aligned}2\log_{b}(5)+\log_{b}(4)&=\log_{b}(5^{2})+\log_{b}(4)\\[1.2em]&=\log_{b}(25)+\log_{b}(4)\\[1.2em]&=\log_{b}(25\times4)\\[1.2em]&=\log_{b}(100)\end{aligned}
c)
\begin{aligned}3\log_{6}(2)+\dfrac{1}{2}\log_{6}(9)&=\log_{6}(2^{3})+\log_{6}(9^{\frac{1}{2}})\\[1.2em]&=\log_{6}(8)+\log_{6}(3)\\[1.2em]&=\log_{6}(8\times3)\\[1.2em]&=\log_{6}(24)\end{aligned}Question 4: Solve 6^{7x}=38, giving your answer to 3 significant figures.
[2 marks]
6^{7x}=38
7x=\log_{6}(38)
x=\dfrac{1}{7}\log_{6}(38)
x=0.290
Question 5: Solve \log_{6}(x-2)+\log_{6}(x-7)=2
[4 marks]
\log_{6}(x-2)+\log_{6}(x-7)=2
\log_{6}((x-2)(x-7))=2
(x-2)(x-7)=6^{2}
x^{2}-9x+14=36
x^{2}-9x-22=0
(x-11)(x+2)=0
x=11 or x=-2
Specification Points Covered
F1 – Know and use the function a^x and its graph, where a is positive
Know and use the function e^x and its graph
F2 – Know that the gradient of e^{kx} is equal to ke^{kx} and hence understand why the exponential model is suitable in many applications
F3 – Know and use the definition of \log_{a}{x} as the inverse of a^x, where a is positive and x ≥ 0
Know and use the function \ln{x} and its graph
Know and use \ln{x} as the inverse function of e^x
F4 – Understand and use the laws of logarithms:
\log_{a}{x} + \log_{a}{y} = \log{a}{(xy)}; \log_{a}{x}-\log_{a}{y}={\left(\dfrac{x}{y}\right)}; k\log_{a}{x}=\log_{a}{x^k}
including, for example, k=-1 and k=-\dfrac{1}{2}
F5 – Solve equations of the form a^x=b
