Moments and Laminas

Note: This topic is not part of the Edexcel spec.

A lamina is simply a flat 2D object with no thickness. For laminae, we wish to find the centre of mass in order to resolve our moments.

Make sure you are happy with the following topics before continuing.

Moments

Pivoting Around the Centre of Mass

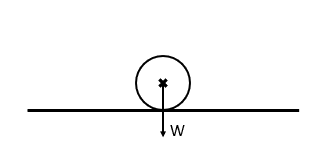
So, for example, say we have a coin balanced on its side. Its centre of mass is right in its centre, so we can conclude that the moments are equal on either side of the coin, and the coin will not rotate.

Now, let’s suggest we have a coin made of copper on one half, and much heavier gold on the other. Clearly, the centre of mass will be skewed towards the heavier gold half.

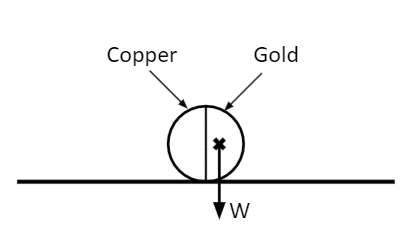
Since the pivot is at the point where the coin meets the surface, the only moment in the system is clockwise, given by the off-centred centre of mass.

The coin will roll until the centre of mass lies directly above the pivot, as this will guarantee that there is no clockwise or anticlockwise moment, and the system will be in equilibrium.

Example: Resolving Moments of Laminae

Say we have a uniform square with weight $\textcolor{red}{700}\text{ N}$ . The square is held up by a piece of rope supplying tension $\textcolor{blue}{T}$ at point $A$ , and its point of tilting is at $D$ . Given that the system is in equilibrium, what is the value of $\textcolor{blue}{T}$ ?

[4 marks]

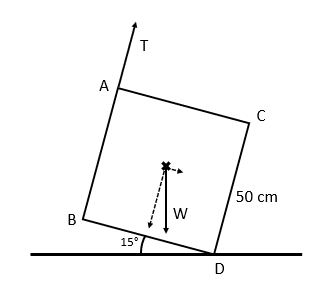
This is a little trickier. When we looked at Moments previously, we assumed that our bodies of mass were on the line of action – that’s no longer the case.

First and foremost, we need to find the centre of mass. Since the square is uniform, the centre of mass is at the centre of the lamina.

Weight now provides both a clockwise and anticlockwise moment.

Clockwise, we now have

$0.25 \times \textcolor{red}{700}\sin 15° + 0.5\textcolor{blue}{T}$

And anticlockwise, we have

$0.25 \times \textcolor{red}{700}\cos 15°$

Since the system is in equilibrium, we have $45.29 + 0.5T = 169.04$ , meaning $\textcolor{blue}{T} = 247.5\text{ N}$ .

Moments and Laminas Example Questions

Question 1: A shop sign is suspended by two pieces of rope at its top corners, $A$ and $B$ . The sign can be modelled as a uniform rectangular lamina with mass $5\text{ kg}$ . If the rope attached at $A$ snaps, what force must be applied horizontally at the corner beneath $B$ , to keep the sign in equilibrium?

[3 marks]

The pivot will be at point $B$ . The centre of mass of the sign is $40\text{ cm}$ along $AB$ .

Therefore, we have:

Anticlockwise: $0.4 \times 5 \times 9.8 = 19.6\text{ N}$

Clockwise: $F$

So we require

$F = 19.6\text{ N}$

Save your answers with

Gold Standard Education

Sign Up Now

Question 2: A $4\text{ cm}$ tall plank of wood is resting on a table. The plank is $40\text{ cm}$ long, with $15\text{ cm}$ off of the table, and uniform. If the plank weighs $150 \text{ N}$ , how many $1\text{ kg}$ weights can be placed on the edge of the plank before it falls over?

[4 marks]

The plank’s centre of mass is $5\text{ cm}$ from the edge of the table, and the edge of the plank is $15\text{ cm}$ from the edge of the table.

Since the system is explicitly perpendicular, we do not need to use trigonometric functions to correct the system.

Take the corner of the table to be our pivot, and let $x$ be the number of $1\text{ kg}$ weights applied.

Clockwise: $0.15 \times 9.8x$

Anticlockwise: $0.05 \times 150 = 7.5\text{ Nm}$ – this is supplied by the centre of mass of the plank.

Setting the two to be equal, we have $7.5 = 1.47x$ , which gives $x = 5.102$ , meaning the system can support $5$ weights. Adding a sixth will violate the equilibrium.

Save your answers with

Gold Standard Education

Sign Up Now