Revise
Geometry Basics Foundation
Geometry Basics: The 5 Simple Rules
Geometry basics will teach you the 5 simple rules needed to answer basic geometry questions, as well as give you the foundations to build as you work through the different geometry topics.
Having basic algebra knowledge is required to solve geometry problems.
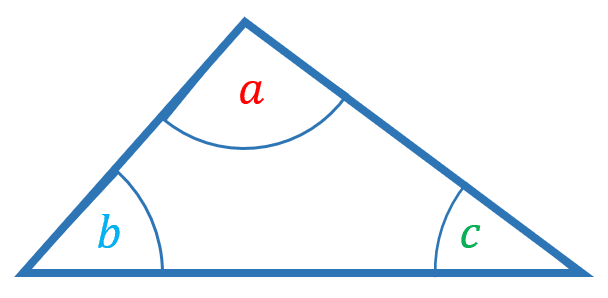
Angles in a triangle add up to 180\degree
The angles in a triangle add up to 180\degree
\textcolor{red}{a} + \textcolor{skyblue}{b} + \textcolor{green}{c} = 180\degree
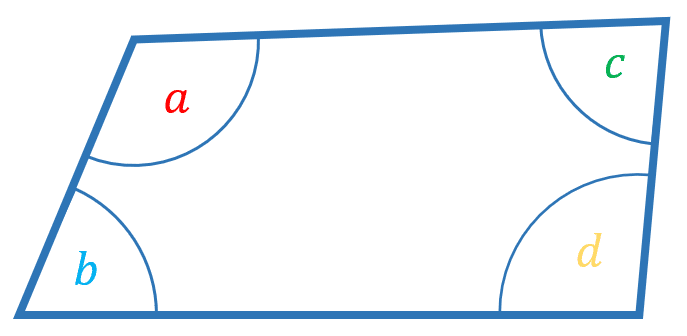
Angles in a quadrilateral add up to 360\degree
The angles in a quadrilateral (4 sided shape) add up to 360\degree
\textcolor{red}{a} + \textcolor{skyblue}{b} + \textcolor{green}{c} + \textcolor{yellow}{d}= 360\degree
Angles on a straight line add up to 180\degree
The angles on a straight line all add up to 180\degree
\textcolor{red}{a} + \textcolor{skyblue}{b} + \textcolor{green}{c} = 180\degree
Angles around a point add up to 360\degree
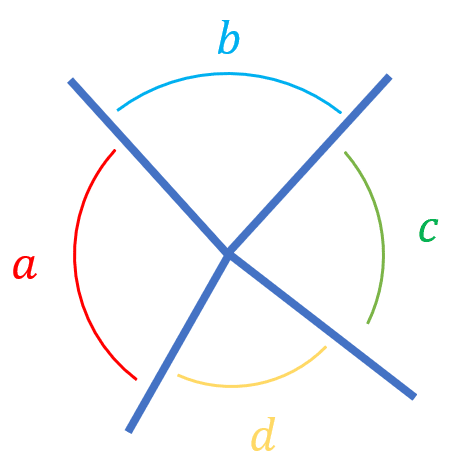
The angles around a point all add up to 360\degree
\textcolor{red}{a} + \textcolor{skyblue}{b} + \textcolor{green}{c} + \textcolor{yellow}{d}= 360\degree
Two sides and two angles of an isosceles triangle are the same
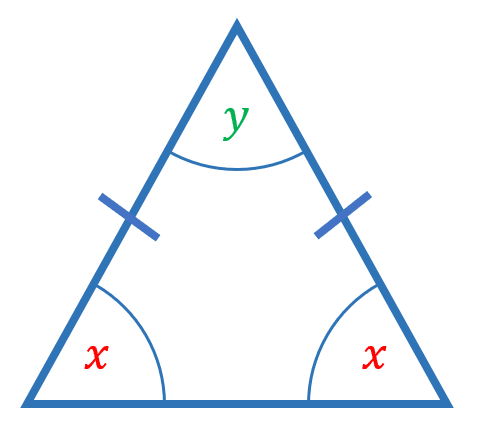
The two sides marked with the lines are the same length.
The two base angles, \textcolor{red}{x}, are the same.
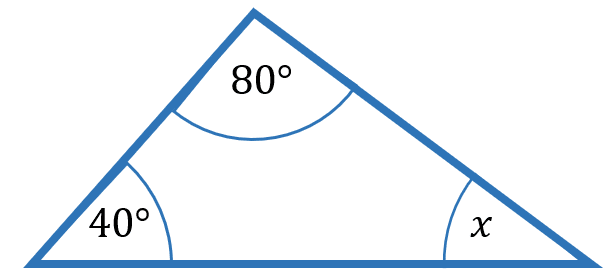
Example 1: Angles in a Triangle
Find the value of x in the triangle shown:
[2 marks]
We know that angles in a triangle add up to 180\degree,
40\degree + 80\degree + x\degree = 180\degree
x= 180\degree -40\degree - 80\degree = 60\degree
x= 60\degree
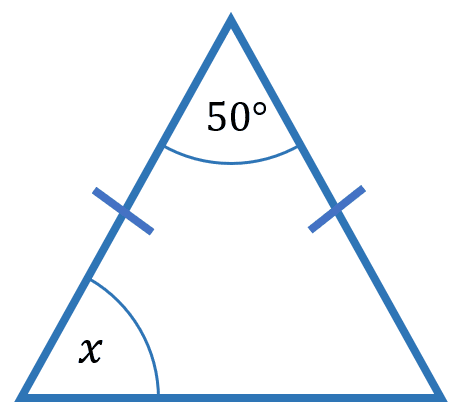
Example 2: Finding a Missing Angle
Find the value of x in the triangle shown:
[2 marks]
We know that in an isosceles triangle, the base angles are equal.
This means we can form the equation:
x\degree + x\degree + 50\degree = 180\degree
2x\degree = 180\degree - 50\degree
2x = 130\degree
x\degree = 65\degree
Geometry Basics Foundation Example Questions
Question 1: Given that the line ADB is a straight line, find the angle CDB shown below.
Give a reason for your answer.
[2 marks]
Angles on a straight line all add together to make 180\degree
\begin{aligned}103\degree+\angle CDB &= 180\degree \\ \angle CDB &= 180\degree-103\degree = 77\degree \end{aligned}
Question 2: A, B, C and D are points around a circle. Find the value of x.
[2 marks] 
Angles around a point all add together to make 360\degree
100\degree+50\degree+x\degree+105\degree =360\degree \\ x=360\degree-100\degree-105\degree-50\degree \\ x= 105\degree
Question 3: DEF is an isosceles triangle. Find the value of y
Give a reason for your answer.
[2 marks]
Base angles in an isosceles triangle are equal and angles in a triangle add up to 180\degree
61\degree+61\degree+y\degree =180\degree \\ y\degree =180\degree-61\degree-61\degree \\ y=58\degree
Question 4: DEF is an isosceles triangle. Find the value of x
Give a reason for your answer.
[2 marks]
Base angles in an isosceles triangle are equal and angles in a triangle add up to 180\degree
\begin{aligned}x+x+55\degree&=180\degree \\ 2x&=180\degree-55\degree = 125\degree \\ x&=\dfrac{125\degree}{2}\end{aligned}
x=62.5\degree
Question 5: ACB forms a triangle shown below. ABD is a straight line.
Find the value of y
Give a reason for your answer.
[3 marks]
Angles on a straight line all add together to make 180\degree so
x=180\degree-115\degree=65\degree
Angles in a triangle add up to 180\degree
y=180\degree-25\degree-65\degree
y=90\degree
Specification Points Covered
Geometry and measures – 3. apply the properties of angles at a point, angles at a point on a straight line, vertically opposite angles; understand and use alternate and corresponding angles on parallel lines; derive and use the sum of angles in a triangle (e.g. to deduce and use the angle sum in any polygon, and to derive properties of regular polygons)
Geometry and measures – 4. derive and apply the properties and definitions of: special types of quadrilaterals, including square, rectangle, parallelogram, trapezium, kite and rhombus; and triangles and other plane figures using appropriate language
Geometry Basics Foundation Worksheet and Example Questions
(NEW) Geometry Problems Foundation Exam Style Questions - MME
Level 1-3GCSENewOfficial MMEGeometry Basics Foundation Drill Questions
Angles - Drill Questions
Level 1-3GCSE
Geometry Problems - Drill Questions
Level 4-5GCSE