Radioactive Half-life

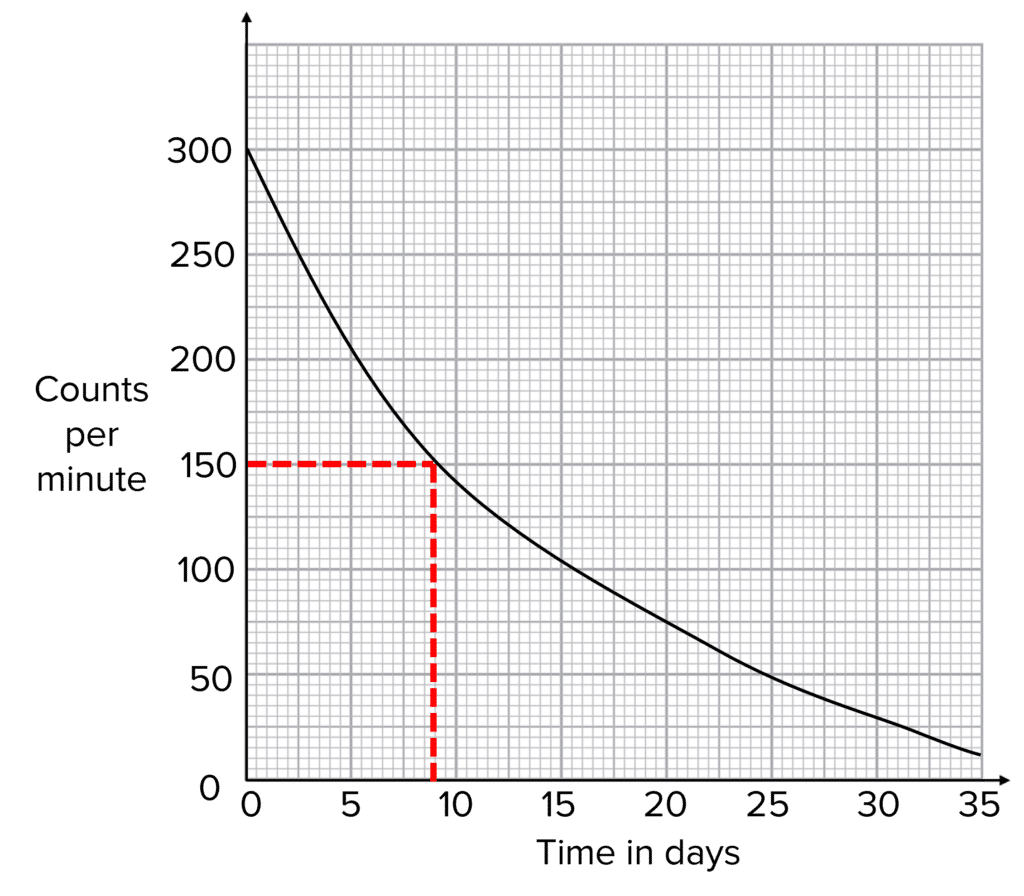
The definition of half-life is the time taken for the count rate from a sample to decrease to half the initial value. If we use a radiation detector, such as a Geiger-Muller tube, we can measure the radiation being emitted from a a sample and calculate the radioactive half life from the results. 

First, you need to plot a graph of the counts per minute against the time. Then, extrapolate the time taken for the counts to reduce by a half. In this example, the original counts was measured to be $300 text{ counts per minute}$ and so half the counts is $150 text{ counts per minute}$. You can see from the graph that this corresponds to $9 text{ days}$. Therefore the half-life of this sample is $9text{ days}$. 

If we know the half-life of a sample we can determine how much smaller the count rate will be after a given number of half-lives. 

For example, after $2text{ half-lives}$, the radioactivity of a sample will be $dfrac{1}{2}times dfrac{1}{2} = bold{color{f21cc2}{dfrac{1}{4}}}$ of the original radioactivity. This is the same as saying it is $4$ times smaller. 

After $3text{ half-lives}$, the radioactivity will be $dfrac{1}{2} times dfrac{1}{2} times dfrac{1}{2} = bold{color{f21cc2}{dfrac{1}{8}}}$ of the original activity, or $8$ times smaller.